1、可微函数
在微积分学中,可微函数是指那些在定义域中所有点都存在导数的函数。可微函数的图像在定义域内的每一点上必存在非垂直切线。因此,可微函数的图像是相对光滑的,没有间断点、尖点或任何有垂直切线的点。
2、锥
锥就是将集合往单方向(元素变大,往正方向放大)放大。
3、可行解、目标值、最优解
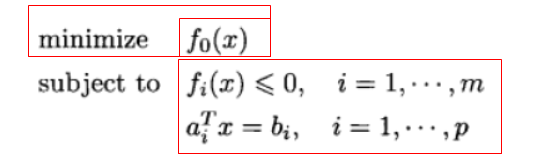
可行解:满足约束条件的解。如上图所示:大方框
目标值:目标函数在可行解上的值为目标值。如上图所示:小方框
最优解:最大目标值点解为最优解。如上图所示:中方框
4、仿射函数
仿射函数即由1阶多项式构成的函数,一般形式为 f (x) = Ax + b,这里,A 是一个 m×k 矩阵,x 是一个 k×1向量,b 是一个 m×1 向量,实际上反映了一种从 k 维到 m 维的空间映射关系。
严格讲,只有 b=0 时,仿射函数才可以叫线性函数。
5、方向箭头的理解
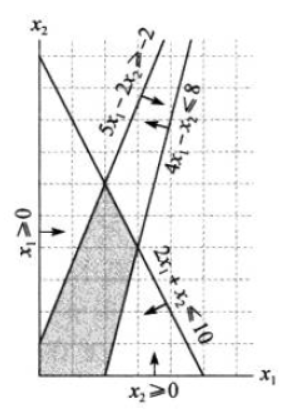
方向箭头可以分解为:x1和x2两个方向。如5x1-2x2=2直线所属的方向可以分解为:+x1,-x2,说明x1变大,而x2变小。
6、单纯形
如果有n个变量,每个约束定义了n维空间中的一个半空间,这些半空间的交集形成的可行区域为单纯形。
补充:
约束就是方向箭头,而方向箭头都可以分解,所以能定义半个空间。
7、标准型和松弛型
在标准型中,所有的约束都是不等式,而在松弛型中,约束都是等式,除非要求变量非负的约束。
在管理运筹学[1]的线性规划模型中,对于“≥”约束条件,可以增加一些代表最低限约束的超过量,称之为剩余变量,从而把“≥”约束条件变为等式约束条件。
线性规划中,一个大于等于约束条件中超过资源或能力最底限的部分称之为剩余量。
2x1 + x2≥400,假如最优解为(150,110)那么剩余量就为10。
线性规划中,小于等于约束条件中未被使用的资源或能力的值成为松弛量。
x1+ x2≤300,假如最优解为(150,140)那么本约束的松弛量就为10。
在线性规划的单纯形法中也会用到此概念。剩余量对应大于等于,松弛量对应小于等于。
补充:
因为不等式能定义半个空间。
8、对偶问题
对偶问题:每一个线性规划问题都伴随有另一个线性规划问题,称为对偶问题。
原始问题:原来的线性规划问题则称为原始线性规划问题,简称原始问题。
对偶问题有许多重要的特征,它的变量能提供关于原始问题最优解的许多重要资料,有助于原始问题的求解和分析。
对偶问题与原始问题之间存在着下列关系:
①目标函数对原始问题是极大化,对偶问题则是极小化。
②原始问题目标函数中的收益系数是对偶问题约束不等式中的右端常数,而原始问题约束不等式中的右端常数则是对偶问题中目标函数的收益系数。
③原始问题和对偶问题的约束不等式的符号方向相反。
④原始问题约束不等式系数矩阵转置后即为对偶问题的约束不等式的系数矩阵。
⑤原始问题的约束方程数对应于对偶问题的变量数,而原始问题的变量数对应于对偶问题的约束方程数。
⑥对偶问题的对偶问题是原始问题,这一性质被称为原始和对偶问题的对称性。
原始问题和对偶问题的标准形式如下,设原始问题为:
min z=cx
s.t. Ax <= b
x>= 0
则对偶问题为:
max w=yb
s.t. yA >= c
y>=0
式中max表示求极大值,min表示求极小值,s.t.表示约束条件;
z为原始问题的目标函数,w为对偶问题的目标函数;
x为原始问题的决策变量列向量(n×1),y为对偶问题的决策变量行向量(1×m);
A为原始问题的系数矩阵(m×n),b为原始问题的右端常数列向量(m×1),c为原始问题的目标函数系数行向量(1×n)。在原始问题与对偶问题之间存在着一系列深刻的关系,现已得到严格数学证明的有如下一些定理:
弱对偶定理
若上述原始问题和对偶问题分别有可行解x0和y0,则cx0<=y0b。这个定理表明极大化问题任一可行解的目标函数值总是不大于它的对偶问题的任一可行解的目标函数值。
强对偶定理
若上述原始问题和对偶问题都可行,则它们分别有最优解x和y,且cx=yb。
最优准则定理
若上述原始问题和对偶问题分别有可行解x0和y0,且两者的目标函数值相等,即y0b=c x0,则两个可行解分别为对应线性规划的最优解。
互补松弛定理
若上述原始问题和对偶问题分别有可行解x0和y0,且u0和v0分别为它们的松弛变量,则当且仅当v0 x0+u0 y0时,x0和y0分别为它们的最优解。

